PERFECTAGØN

How to Draw N-Sided Regular Polygons
Compass Ø Straightedge Construction

Intro

Divide Line

Standard Setup

Perfectagon Base

Established Methods

 

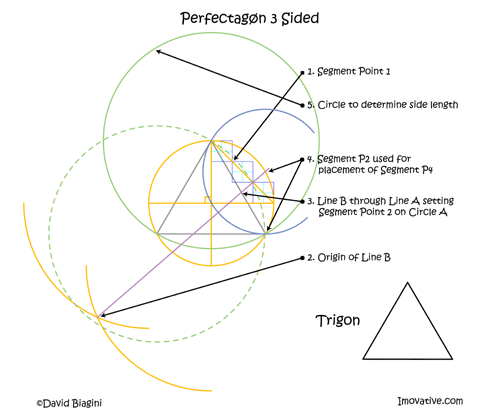
The next diagram reveals how to utilize Perfectagøn to create a trigon.

A good aspect to note is that the divisions along the diagonal line, Line A, can be extended perpendicular to the crossed lines within Circle A. Therefore it should become very apparent how graph paper can be used to help save the steps of dividing Line A with the compass and straightedge. But if you don't have graph paper you can still divide the line equally.

Since Perfectagøn basically divides one quarter of Circle A into the number of segments equaling the number of sides for the target regular polygon, Line B would ideally intersect segment four-four times segment one. The trigon has only three sides, therefore three segments. The issue of having to work with the fourth segment is solved by simply intersecting the second segment and using the intersection on Circle A as the center of the circle used to determine where the fourth segment point would theoretically intersect on Circle A. An alternative to this way is to utilize Perfectagøn for the hexagon and connecting the necessary points to create the trigon.